DL基础-神经网络的批标准化
作者|Emrick Sinitambirivoutin
编译|VK
来源|Towards Data Science

训练学习系统的一个主要假设是在整个训练过程中输入分布是保持不变的。对于简单地将输入数据映射到某些适当输出的线性模型,这种条件总是能满足的,但在处理由多层叠加而成的神经网络时,情况就不一样了。
在这样的体系结构中,每一层的输入都受到前面所有层参数的影响(随着网络变得更深,对网络参数的小变化会被放大),因此,在一层内的反向传播步骤中所做的一个小的变化可以产生另一层输入的一个巨大变化,并在最后改变特征的映射分布。在训练过程中,每一层都需要不断地适应前一层得到的新分布,这就减慢了收敛速度。
批标准化克服了这一问题,同时减少了训练过程中内层的协方差移位(由于训练过程中网络参数的变化而导致的网络激活分布变化)
本文将讨论以下内容
- 批标准化如何减少内部协方差移位,如何改进神经网络的训练。
- 如何在PyTorch中实现批标准化层。
- 一些简单的实验展示了使用批标准化的优点。
减少内部协方差移位
减少神经网络内部协方差移位的不良影响的一种方法是对层输入进行归一化,这个操作不仅使输入具有相同的分布,而且还使每个输入都白化(白化是对原始数据x实现的一种变换,使变换之后数据的协方差矩阵为单位阵),该方法是由一些相关研究提出的,这些研究表明,如果对网络的输入进行白化,则网络训练收敛得更快,因此,增强各层输入的白化是网络的一个理想特性。
然而,每一层输入的完全白化是昂贵的,并且不是完全可微的。批标准化通过考虑两个假设克服了这个问题:
- 我们将独立地对每个标量特征进行归一化(通过设置均值为0和方差为1),而不是对层的输入和输出的特征进行白化。
- 我们不使用整个数据集来进行标准化,而是使用mini-batch,每个mini-batch生成每个激活层的平均值和方差的估计值。
对于具有d维输入的层x = (x1, x2, ..xd),我们得到了以下归一化公式(对batch B的期望和方差进行计算):

然而,简单地标准化一个层的每个输入可能会改变层所能表示的内容。例如,对一个sigmoid的输入进行归一化会将其约束到非线性的线性状态,这样的行为对网络来说是不可取的,因为它会降低其非线性的能力(它会相当于一个单层网络)。
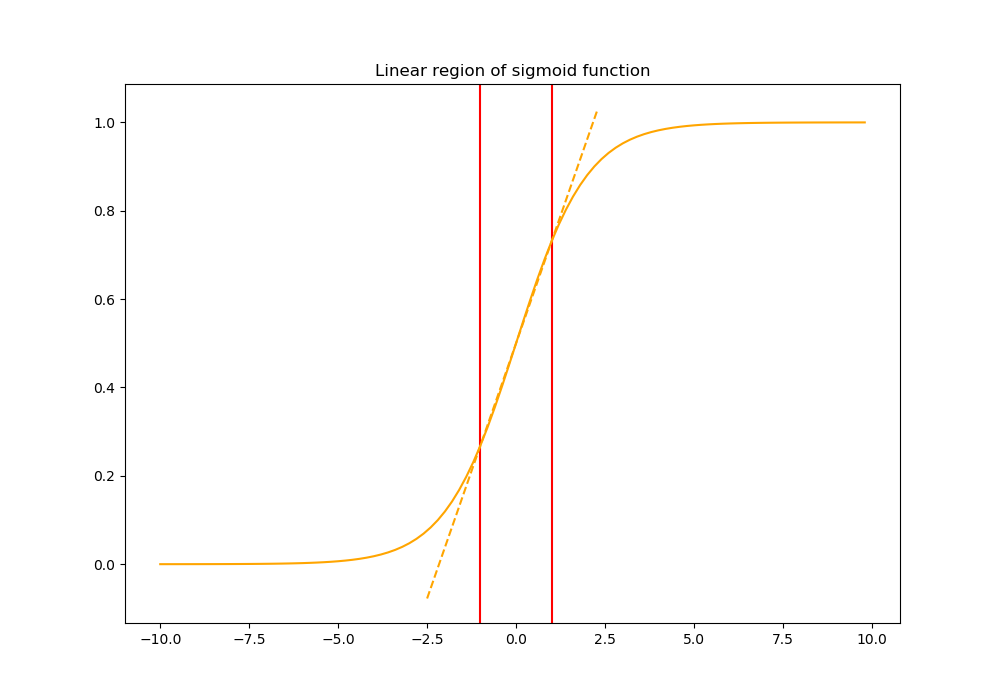
为了解决这个问题,批标准化确保了插入到网络中的转换可以表示为单位转换(模型仍然在每个层学习到一些参数,这些参数在没有线性映射的情况下调整从上一层接收到的激活),这是通过引入一对可学习参数gamma_k和beta_k来实现的,这两个参数根据模型学习的内容进行缩放和移动标准化值。
最后,得到的层的输入(基于前一层的输出x)为:

批标准化算法
训练时
全连接层
全连接层的实现非常简单。我们只需要得到每个批次的均值和方差,然后用之前给出的alpha和beata参数来缩放和移动。
在反向传播期间,我们将使用反向传播来更新这两个参数。
mean = torch.mean(X, axis=0)
variance = torch.mean((X-mean)**2, axis=0)
X_hat = (X-mean) * 1.0 /torch.sqrt(variance + eps)
out = gamma * X_hat + beta卷积层
卷积层的实现几乎与以前一样,我们只需要执行一些改造,以适应我们从上一层获得的输入结构。
N, C, H, W = X.shape
mean = torch.mean(X, axis = (0, 2, 3))
variance = torch.mean((X - mean.reshape((1, C, 1, 1))) ** 2, axis=(0, 2, 3))
X_hat = (X - mean.reshape((1, C, 1, 1))) * 1.0 / torch.sqrt(variance.reshape((1, C, 1, 1)) + eps)
out = gamma.reshape((1, C, 1, 1)) * X_hat + beta.reshape((1, C, 1, 1))在PyTorch中,反向传播非常容易处理,这里一件重要事情是指定alpha和beta在反向传播阶段更新它们的参数。
为此,我们将在层中将它们声明为nn.Parameter(),并使用随机值初始化它们。
推理时
在推理过程中,我们希望网络的输出只依赖于输入,因此我们不能考虑之前考虑mini-batch的统计数据(它们与mini-batch大小相关,因此它们根据数据而变化)。为了确保我们有一个固定的期望和方差,我们需要使用整个数据集来计算这些值,而不是只考虑mini-batch,然而,就时间和计算而言,为所有数据集计算这些统计信息是相当昂贵的。
论文中提出的方法是使用我们在训练期间计算的滑动统计,我们使用参数beta(动量)调整当前批次计算的期望重要性:
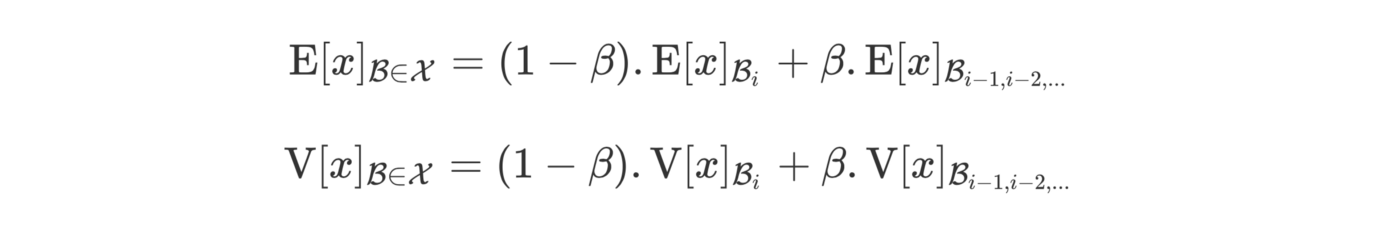
该滑动平均值存储在一个全局变量中,该全局变量在训练阶段更新。
为了在训练期间将这个滑动平均值存储在我们的层中,我们可以使用缓冲区,当我们使用PyTorch的register_buffer()方法实例化我们的层时,我们将初始化这些缓冲区。
最后一个模块
最后一个模块由前面描述的所有块组成。我们在输入数据的形状上添加一个条件,以了解我们处理的是全连接层还是卷积层。
这里需要注意的一件重要事情是,我们只需要实现forward()方法,因为我们的类继承自nn.Module,我们就可以自动得到backward()函数。
class CustomBatchNorm(nn.Module):
def __init__(self, in_size, momentum=0.9, eps = 1e-5):
super(CustomBatchNorm, self).__init__()
self.momentum = momentum
self.insize = in_size
self.eps = eps
U = uniform.Uniform(torch.tensor([0.0]), torch.tensor([1.0]))
self.gamma = nn.Parameter(U.sample(torch.Size([self.insize])).view(self.insize))
self.beta = nn.Parameter(torch.zeros(self.insize))
self.register_buffer('running_mean', torch.zeros(self.insize))
self.register_buffer('running_var', torch.ones(self.insize))
self.running_mean.zero_()
self.running_var.fill_(1)
def forward(self, input):
X = input
if len(X.shape) not in (2, 4):
raise ValueError("only support dense or 2dconv")
#全连接层
elif len(X.shape) == 2:
if self.training:
mean = torch.mean(X, axis=0)
variance = torch.mean((X-mean)**2, axis=0)
self.running_mean = (self.momentum * self.running_mean) + (1.0-self.momentum) * mean
self.running_var = (self.momentum * self.running_var) + (1.0-self.momentum) * (input.shape[0]/(input.shape[0]-1)*variance)
else:
mean = self.running_mean
variance = self.running_var
X_hat = (X-mean) * 1.0 /torch.sqrt(variance + self.eps)
out = self.gamma * X_hat + self.beta
# 卷积层
elif len(X.shape) == 4:
if self.training:
N, C, H, W = X.shape
mean = torch.mean(X, axis = (0, 2, 3))
variance = torch.mean((X - mean.reshape((1, C, 1, 1))) ** 2, axis=(0, 2, 3))
self.running_mean = (self.momentum * self.running_mean) + (1.0-self.momentum) * mean
self.running_var = (self.momentum * self.running_var) + (1.0-self.momentum) * (input.shape[0]/(input.shape[0]-1)*variance)
else:
mean = self.running_mean
var = self.running_var
X_hat = (X - mean.reshape((1, C, 1, 1))) * 1.0 / torch.sqrt(variance.reshape((1, C, 1, 1)) + self.eps)
out = self.gamma.reshape((1, C, 1, 1)) * X_hat + self.beta.reshape((1, C, 1, 1))
return out实验MNIST
为了观察批处理归一化对训练的影响,我们可以比较没有批处理归一化的简单神经网络和有批处理归一化的神经网络的收敛速度。
为了简单起见,我们在MNIST数据集上训练这两个简单的全连接网络,不进行预处理(只应用数据标准化)。
没有批标准化的网络架构
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.classifier = nn.Sequential(
nn.Linear(28 * 28, 64),
nn.ReLU(),
nn.Linear(64, 128),
nn.ReLU(),
nn.Linear(128, 10)
)
def forward(self, x):
x = x.view(x.size(0), -1)
x = self.classifier(x)
return x有批标准化的网络架构
class SimpleNetBN(nn.Module):
def __init__(self):
super(SimpleNetBN, self).__init__()
self.classifier = nn.Sequential(
nn.Linear(28 * 28, 64),
CustomBatchNorm(64),
nn.ReLU(),
nn.Linear(64, 128),
CustomBatchNorm(128),
nn.ReLU(),
nn.Linear(128, 10)
)
def forward(self, x):
x = x.view(x.size(0), -1)
x = self.classifier(x)
return x结果
下图显示了在我们的SimpleNet的第一层之后获得的激活分布,我们可以看到,即使经过20个epoch,分布仍然是高斯分布(在训练过程中学习到的小尺度和移位)。
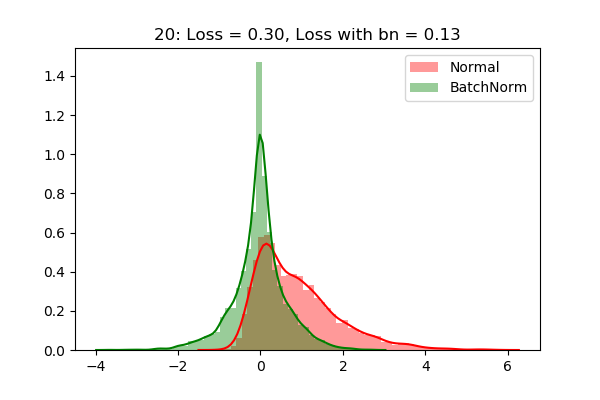
我们也可以看到收敛速度方面的巨大进步。绿色曲线(带有批标准化)表明,我们可以更快地收敛到具有批标准化的最优解。
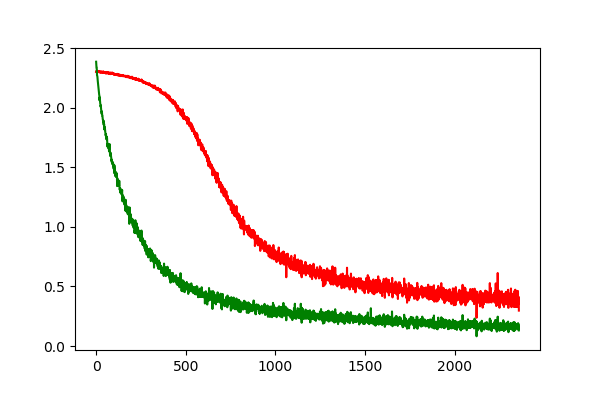
实验结果详见(https://github.com/sinitame/neuralnetworks-ents/blob/master/batch_normalization/batch_normaliz.ipynb)
结论
使用批标准化进行训练的优点
- 一个mini-batch处理的损失梯度是对训练集梯度的估计,训练的质量随着批处理大小的增加而提高。
- 由于gpu提供的并行性,批处理大小上的计算要比单个示例的多次计算效率高得多。
- 在每一层使用批处理归一化来减少内部方差的移位,大大提高了网络的学习效率。
原文链接:https://towardsdatascience.com/understanding-batch-normalization-for-neural-networks-1cd269786fa6
未经允许不得转载,请联系zhouas@hotmail.com获取授权:目标检测 » DL基础-神经网络的批标准化
 目标检测
目标检测
